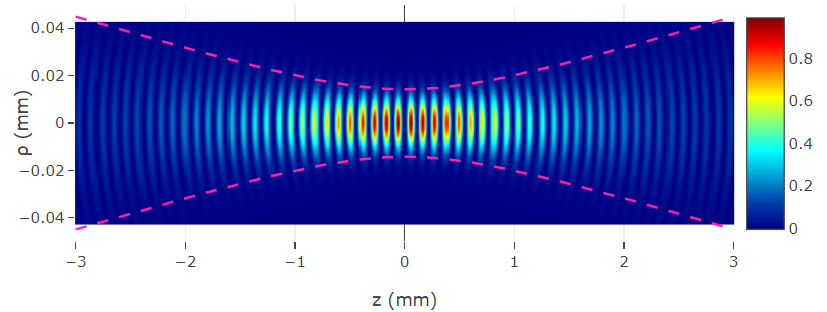
Gaussian beam
Paraxial wave can be viewed as a slowly varying envelope traveling along the z direction maintaining the properties of the plane wave, $$ U(\textbf{r}) = A(\textbf{r}) exp(-jkz) $$ The solution of paraxial wave should satisfy the paraxial Helmholtz equation is, $$ \nabla_{T}^{2}A - j2k\dfrac{\partial A}{\partial z} = 0 $$ One of the simplest solution is paraboloidal wave, $$ A(\textbf{r}) = \dfrac{A_{1}}{z} exp \left(-jk \dfrac{\rho^{2}}{2z} \right), \quad \rho^{2} = x^{2} + y^{2} $$
If the paraboloidal wave is centered about the point \(z=\xi\), it still satisfies the paraxial Helmholtz equation. Moreover, it also holds when \(\xi\) is complex value. Then we can set \(\xi=-jz_{0}\), a purely imaginary for exponentially decay. Thus, we can replace \(z\) as \(q(z)=z+jz_{0}\), then the paraboloidal wave can be written as, $$ A(\textbf{r}) = \dfrac{A_{1}}{q(z)} exp \left(-jk \dfrac{\rho^{2}}{2q(z)} \right), \quad q(z)=z+jz_{0} $$ The quantity \(q(z)\) is defined as the q-parameter, and the \(z_{0}\) is known as the Rayleigh range. If we separate the real part and imaginary part of the q-parameter as two real functions, we get $$ \dfrac{1}{q(z)} = \dfrac{1}{R(z)} - j\dfrac{\lambda}{\pi W^{2}(z)} $$ where \(R(z)\) is defined as the wavefront radius of curvature and \(W(z)\) is defined as the beam width. Finally, if we replace \(q(z)\) as the function of \(W(z)\) and \(R(z)\) in paraxial Helmholtz equation, then the expression for the complex amplitude of the Gaussian beam is, $$ U(r) = A_{0} \dfrac{W_{0}}{W(z)} exp\left[-\dfrac{\rho^2}{W^2(z)}\right] exp\left[-jkz - jk\dfrac{\rho^2}{2R(z)} + j\zeta(z)\right] $$
The intensity of the Gaussian beam \(I(\rho, z) = \left| U(r) \right|^2\) is, \begin{align} I(\rho, z) &= \left| A_{0} \right|^2 \left[\dfrac{W_{0}}{W(z)}\right]^2 exp\left[-\dfrac{2\rho^2}{W^2(z)}\right] \end{align}
- Rayleigh range
- Beam waist
- Beam width
- Wavefront radius of curvature
- Gouy phase
- Intensity on the beam axis \(I(\rho=0,z)\)
- Intensity at the transverse plane \(I(x,y,z=0)\)
- Intensity at y-z plane \(I(x=0,y,z)\)
- Intensity at the y-z plane \(I(x=0,y,z,t=t_{0})\) at an instant of time
- Intensity 3D plot
$$ z_{0} = \dfrac{\pi W_{0}^2}{\lambda} $$
$$ W_{0} = \sqrt{\dfrac{\lambda z_{0}}{\pi}} $$
$$ W(z) = \sqrt{\dfrac{\lambda z_{0}}{\pi}} \sqrt{1 + \left(\dfrac{z}{z_{0}}\right)^2} = W_{0} \sqrt{1 + \left(\dfrac{z}{z_{0}}\right)^2} \\ $$ The minimum value \(W_{0}\) of beam width occurs when \(z=0\), where it is known as the waist radius, and the spot size is defined as \(2W_{0}\).
As the \(z\) is large enough (\(z \gg z_{0}\)) so that the beam width can be approximated by an asymptote, $$W(z) \approx \dfrac{W_{0}}{z_{0}}z = \dfrac{W_{0}}{W_{0}^{2}\pi / \lambda}z = \left(\dfrac{\lambda}{\pi W_{0}}\right) z = \theta_{0}z$$ where we define the angular divergence of the beam is, $$\Theta = 2\theta_{0} = \dfrac{4}{\pi}\left(\dfrac{\lambda}{2W_{0}}\right).$$
At the plane \(z=0\), the minimum spot area is \(\pi W_{0}^{2}\), where is the best focus. While the spot area would gradually increase beyond the plane \(z=0\). The spot area reach twice size of \(\pi W_{0}^{2}\) when \(W=\sqrt{2}W_{0}\) at \(z=z_{0}\), then we defined the depth-of-focus is, $$2z_{0} = \dfrac{2\pi W_{0}^2}{\lambda}.$$
$$ R(z) = z \left[1 + \left(\dfrac{z_{0}}{z}\right)^2\right] $$
The wavefront radius of curvature has a minimum value \(2z_{0}\) at \(z=z_{0}\). As \(z\) is larger than \(z_{0}\) (\(z \gg z_{0}\)), the curvature can be approximated by \(R(z) \approx z\), which indicates the wavefront of a spherical wave. As \(z\) approaches to \(z=0\) from positive side, the curvature would approach to infinity, which indicates the wavefront of a planar wave.
$$ \zeta(z) = tan^{-1}\left(\dfrac{z}{z_{0}}\right) $$
$$ I(\rho=0, z) = \left| A_{0} \right|^2 \left[\dfrac{W_{0}}{W(z)}\right]^2 = \dfrac{\left| A_{0} \right|^2}{1+\left(\dfrac{z}{z_{0}}\right)^{2}} $$ Assume \(I_{0}=\left| A_{0} \right|^2\), then the normalized intensity on the beam axis can be expressed as, $$ \dfrac{I(\rho=0, z)}{I_{0}} = \dfrac{1}{1+\left(\dfrac{z}{z_{0}}\right)^{2}} $$ We can find that the intensity has a maximum value at \(\rho=0\), and then gradually decreases as \(\rho\) gets greater.
Hermite-Gaussian beam
The complex amplitude of Hermite-Gaussian beam has the form, \begin{align} U_{l,m}(x,y,z) = A_{l,m} \left[ \dfrac{W_{0}}{W(z)}\right] \mathbb{G}_{l}\left[\dfrac{\sqrt{2}x}{W(z)}\right] \mathbb{G}_{m}\left[\dfrac{\sqrt{2}y}{W(z)}\right] \\ \times exp\left[-jkz - jk\dfrac{x^2+y^2}{2R(z)} + j(l+m+1)\zeta(z)\right] \end{align}

- Hermite-Gaussian polynomial
- Intensity at the transverse plane \(I(x,y,z=0)\)
Hermite polynomial $$ \mathbb{H}_{l+1}(u) = 2u \mathbb{H}_{l}(u) - 2l\mathbb{H}_{l-1}(u) ,\:\text{where} \; \mathbb{H}_{0}(u)=1, \; and \; \mathbb{H}_{1}(u)=2u $$
The intensity of the Hermite-Gaussian beam \(I_{l,m} = \left| U_{l,m} \right|^2\) is, $$ I_{l,m}(x,y,z) = \left|A_{l,m}\right|^2 \left[ \dfrac{W_{0}}{W(z)}\right]^2 \mathbb{G}_{l}^2\left[\dfrac{\sqrt{2}x}{W(z)}\right] \mathbb{G}_{m}^2\left[\dfrac{\sqrt{2}y}{W(z)}\right] $$
Laguerre-Gaussian beam
The complex amplitude of Laguerre-Gaussian beam has the form, \begin{align} U_{l,m}(\rho,\phi,z) = A_{l,m} \left[ \dfrac{W_{0}}{W(z)}\right] \left( \dfrac{\rho}{W(z)}\right)^{l} \mathbb{L}^{l}_{m}\left(\dfrac{2\rho^{2}}{W^{2}(z)}\right) exp\left(-\dfrac{\rho^{2}}{W^{2}(z)}\right) \\ \times exp\left[-jkz - jk\dfrac{\rho^{2}}{2R(z)} \mp{jl\phi}+ j(l+2m+1)\zeta(z)\right] \end{align}
The intensity of the Laguerre-Gaussian beam \(I_{l,m} = \left| U_{l,m} \right|^2\) is, $$ I_{l,m}(\rho,\phi,z) = \left|A_{l,m}\right|^{2} \left[ \dfrac{W_{0}}{W(z)}\right]^{2} \left( \dfrac{\rho}{W(z)}\right)^{2l} {\mathbb{L}^{l}_{m}}^{2}\left(\dfrac{2\rho^{2}}{W^{2}(z)}\right) exp\left(-\dfrac{2\rho^{2}}{W^{2}(z)}\right) $$
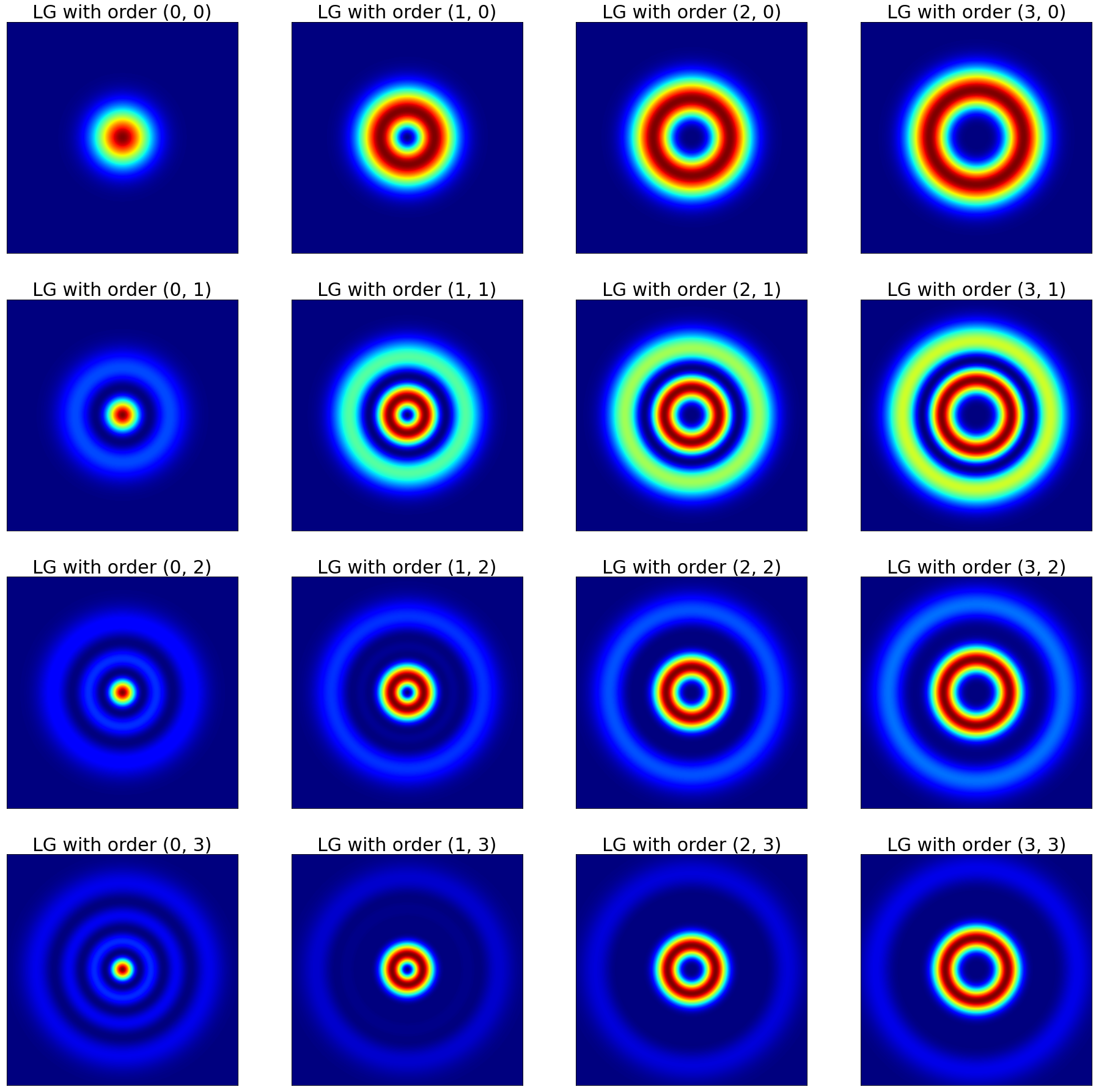
- Generalized Laguerre polynomial
- Intensity at the transverse plane \(I(x,y,z=0)\)
\begin{align} \mathbb{L}^{l}_{m+1}(u) = \dfrac{(2m+1+l-u)\mathbb{L}^{l}_{m}(u) - (m+l)\mathbb{L}^{l}_{m-1}(u)}{m+1} , \\ \:\text{where} \; \mathbb{L}^{l}_{0}(u) = 1 \; and \; \mathbb{L}^{l}_{1}(u) = 1 + l - u \end{align}
References
- A., S., & Teich, M. (2019). Fundamentals of photonics. John Wiley & Sons.